The psycheval package is a set of functions that can be useful in psychological evaluations. It accompanies the Individual Psychometrics online textbook.
Installation
You can install the development version of psycheval like so:
remotes::install_github("wjschne/psycheval")Convert a variable to standard scores
Suppose you have a scaled score of 12 (μ = 10, σ = 3) that you want to convert to a standard score (μ = 100, σ = 15).
library(psycheval)
x2standard(12, mu_x = 10, sigma_x = 3)
#> [1] 110To convert to a z-score (μ = 0, σ = 1):
x2standard(12,
mu_x = 10, sigma_x = 3,
mu_new = 0, sigma_new = 1)
#> [1] 0.67To convert to T-score (μ = 50, σ = 10):
x2standard(12,
mu_x = 10, sigma_x = 3,
mu_new = 50, sigma_new = 10)
#> [1] 57Covariance of weighted sums
Let’s create a covariance matrix of 5 variables that all correlate at .60.
# Create covariance matrix
Sigma <- matrix(0.6, nrow = 5, ncol = 5)
diag(Sigma) <- 1
Sigma
#> [,1] [,2] [,3] [,4] [,5]
#> [1,] 1.0 0.6 0.6 0.6 0.6
#> [2,] 0.6 1.0 0.6 0.6 0.6
#> [3,] 0.6 0.6 1.0 0.6 0.6
#> [4,] 0.6 0.6 0.6 1.0 0.6
#> [5,] 0.6 0.6 0.6 0.6 1.0Suppose we want to create a sum of the first 2 variables and a sum of the remaining three variables. What would the covariance matrix of the summary variables be?
First we create a weight matrix w with 5 rows and 2 columns consisting entirely of zeros. The first column represents the weight for the first variable. We put ones in the first two rows of the first column and ones in rows 3–5 in the second column.
# Create weight matrix
w <- matrix(0, nrow = 5, ncol = 2)
w[1:2,1] <- 1
w[3:5,2] <- 1
w
#> [,1] [,2]
#> [1,] 1 0
#> [2,] 1 0
#> [3,] 0 1
#> [4,] 0 1
#> [5,] 0 1The covariance matrix of the sums is:
# covariance matrix of weighted sums
composite_covariance(Sigma, w)
#> [,1] [,2]
#> [1,] 3.2 3.6
#> [2,] 3.6 6.6To include the original variables in the covariance matrix, append an identity matrix to w:
# A 5 by 5 idendity matrix
I <- diag(5)
I
#> [,1] [,2] [,3] [,4] [,5]
#> [1,] 1 0 0 0 0
#> [2,] 0 1 0 0 0
#> [3,] 0 0 1 0 0
#> [4,] 0 0 0 1 0
#> [5,] 0 0 0 0 1
# Prepend the identity matrix to the w matrix
w_expanded <- cbind(diag(5), w)
w_expanded
#> [,1] [,2] [,3] [,4] [,5] [,6] [,7]
#> [1,] 1 0 0 0 0 1 0
#> [2,] 0 1 0 0 0 1 0
#> [3,] 0 0 1 0 0 0 1
#> [4,] 0 0 0 1 0 0 1
#> [5,] 0 0 0 0 1 0 1
# Covariance matrix of original variables and the summary variables
BigSigma <- composite_covariance(Sigma, w_expanded)
BigSigma
#> [,1] [,2] [,3] [,4] [,5] [,6] [,7]
#> [1,] 1.0 0.6 0.6 0.6 0.6 1.6 1.8
#> [2,] 0.6 1.0 0.6 0.6 0.6 1.6 1.8
#> [3,] 0.6 0.6 1.0 0.6 0.6 1.2 2.2
#> [4,] 0.6 0.6 0.6 1.0 0.6 1.2 2.2
#> [5,] 0.6 0.6 0.6 0.6 1.0 1.2 2.2
#> [6,] 1.6 1.6 1.2 1.2 1.2 3.2 3.6
#> [7,] 1.8 1.8 2.2 2.2 2.2 3.6 6.6
# Convert to correlations with the cov2cor function
composite_covariance(Sigma, w_expanded, correlation = T)
#> [,1] [,2] [,3] [,4] [,5] [,6] [,7]
#> [1,] 1.0000 0.6000 0.6000 0.6000 0.6000 0.8944 0.7006
#> [2,] 0.6000 1.0000 0.6000 0.6000 0.6000 0.8944 0.7006
#> [3,] 0.6000 0.6000 1.0000 0.6000 0.6000 0.6708 0.8563
#> [4,] 0.6000 0.6000 0.6000 1.0000 0.6000 0.6708 0.8563
#> [5,] 0.6000 0.6000 0.6000 0.6000 1.0000 0.6708 0.8563
#> [6,] 0.8944 0.8944 0.6708 0.6708 0.6708 1.0000 0.7833
#> [7,] 0.7006 0.7006 0.8563 0.8563 0.8563 0.7833 1.0000Compute a composite score
Suppose we have two subtest scores A = 12 and B = 14. Both scores are on the scaled score metric (μ = 10, σ = 3). We want to create a composite score on the standard score metric (μ = 100, σ = 15).
The subtests A and B correlated at ρ = .6.
# Subtest scores
x <- c(12, 14)
# Subtest correlation
rho <- 0.6
# Subtest correlation matrix
R <- matrix(c(1,rho, rho, 1), ncol = 2)
# Compute composite score
composite_score(x = x,
R = R,
mu_x = 10,
sigma_x = 3,
mu_composite = 100,
sigma_composite = 15)
#> [1] 116.8Compute a multivariate confidence interval conditioned on a set of observed scores
library(readr)
library(ggplot2)
library(dplyr)
#>
#> Attaching package: 'dplyr'
#> The following objects are masked from 'package:stats':
#>
#> filter, lag
#> The following objects are masked from 'package:base':
#>
#> intersect, setdiff, setequal, union
# Observed scores
x_wisc <- c(
vci = 130,
vsi = 120,
fri = 123,
wmi = 116,
psi = 97)
# Reliability coefficients
rxx_wisc <- c(
vci = .92,
vsi = .92,
fri = .93,
wmi = .92,
psi = .88)
# Correlation matrix
R_wisc <- ("
index vci vsi fri wmi psi
vci 1.00 0.59 0.59 0.53 0.30
vsi 0.59 1.00 0.62 0.50 0.36
fri 0.59 0.62 1.00 0.53 0.31
wmi 0.53 0.50 0.53 1.00 0.36
psi 0.30 0.36 0.31 0.36 1.00") |>
read_tsv(col_types = cols(
.default = col_double(),
index = col_character())) |>
tibble::column_to_rownames("index") |>
as.matrix()
R_wisc
#> vci vsi fri wmi psi
#> vci 1.00 0.59 0.59 0.53 0.30
#> vsi 0.59 1.00 0.62 0.50 0.36
#> fri 0.59 0.62 1.00 0.53 0.31
#> wmi 0.53 0.50 0.53 1.00 0.36
#> psi 0.30 0.36 0.31 0.36 1.00
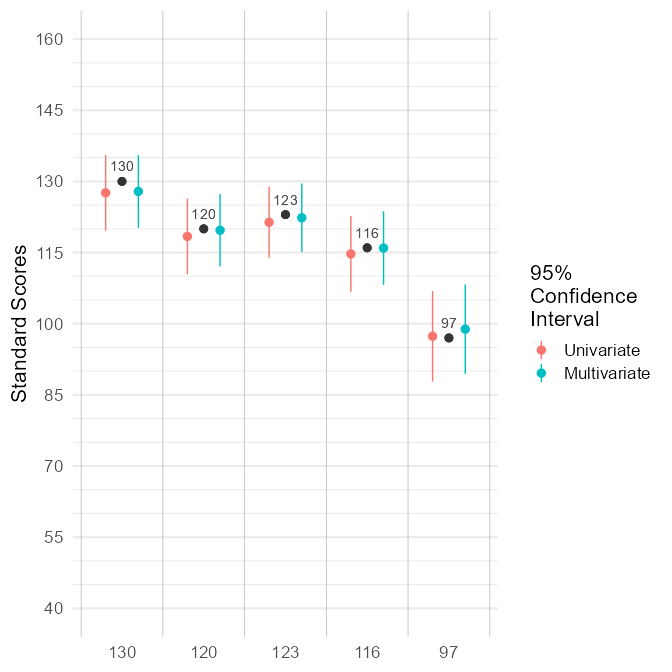
d_ci <- multivariate_ci(
x = x_wisc,
r_xx = rxx_wisc,
mu = rep(100, 5),
sigma = R_wisc * 225)
d_ci
#> variable x r_xx mu_univariate see_univariate mu_multivariate
#> vci vci 130 0.92 127.60 4.069 127.88
#> vsi vsi 120 0.92 118.40 4.069 119.70
#> fri fri 123 0.93 121.39 3.827 122.33
#> wmi wmi 116 0.92 114.72 4.069 115.95
#> psi psi 97 0.88 97.36 4.874 98.86
#> see_multivariate upper_univariate lower_univariate upper_multivariate
#> vci 3.912 135.6 119.62 135.5
#> vsi 3.897 126.4 110.42 127.3
#> fri 3.685 128.9 113.89 129.6
#> wmi 3.954 122.7 106.74 123.7
#> psi 4.803 106.9 87.81 108.3
#> lower_multivariate
#> vci 120.21
#> vsi 112.07
#> fri 115.11
#> wmi 108.20
#> psi 89.44Compare the multivariate CI to the univariarte CI:
Relative Proficiency Index
When a typical same-age peer with an ability of W = 500 has a .90 probability of answering a question correctly, what is the probability that a person with ability of W = 520 will answer the question correctly?
rpi(x = 520, mu = 500)
#> 0.9878Flipping the previous question, when a person with ability of W = 520 has a .90 probability of answering a question correctly, what is the probability that a typical same-age peer with an ability of W = 500 will answer the question correctly?
rpi(x = 520, mu = 500, reverse = TRUE)
#> 0.5Criteria other than .9 proficiency are also possible. For example, when a typical same-age peer with an ability of W = 500 has a .25 probability of answering a question correctly, what is the probability that a person with ability of W = 520 will answer the question correctly?
rpi(x = 520, mu = 500, criterion = .25)
#> 0.75